Análisis Discriminante Lineal es un algoritmo de machine learning que nos permite la clasificación multi-clase de datos, permitiendo la predicción de campos polinomiales.
Características del modelo:
Usos: Clasificación polinómica (categórica)
Explicación Breve: Utiliza probabilidades de los atributos respecto el objetivo para predecir. Usa Bayes
Cualidades:
- Se asume distribuciones gaussianas de atributos
- Se asume misma varianza para todos los atributos
Preparación de Datos:
- Eliminar Outliers
- Requiere una distribución normal/gaussiana en todos los atributos
- Conviene estandarizar (para tener Media=0 y Varianza=1)
En el presente trabajo demostraremos un proceso básico de este algoritmo en Python con SciKit Learn.
Análisis preliminar de Datos
Utilizaremos un conjunto de datos reducido, con parámetros abstractos.
| Atributo | Tipo |
|---|---|
| X | integer |
| Y | integer |
| Label (var objetivo) | polinomial |
Procedimiento en Python
Primero importamos librerías y cargamos el dataset.
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import ConfusionMatrixDisplay, classification_report
from sklearn.model_selection import train_test_split
input_file = "sample.csv"
df = pd.read_csv(input_file, header=0)
df.sample(n=5)
| x | y | label | |
|---|---|---|---|
| 13 | 8.375419 | 0.520687 | 1 |
| 8 | 1.088070 | 1.150220 | 0 |
| 0 | 2.781084 | 2.550537 | 0 |
| 11 | 5.332441 | 2.088627 | 1 |
| 17 | 5.922597 | 1.881064 | 1 |
Podemos visualizarlos mejor con SKLearn
colors = ("orange", "blue")
plt.scatter(df['x'], df['y'], s=300, c=df['label'],
cmap=matplotlib.colors.ListedColormap(colors))
plt.show()
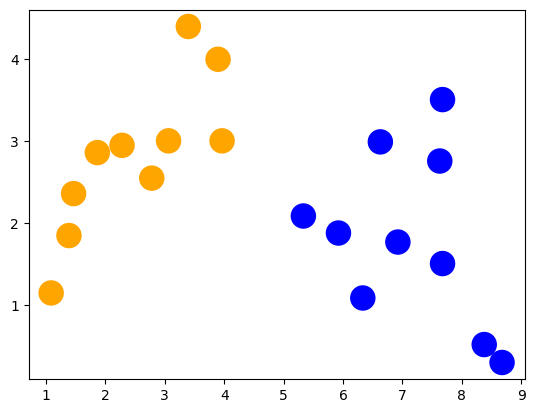
Separamos las entradas de la salida y dividimos los datos para entrenar y testear.
X = df[['x', 'y']].values
y = df['label'].values
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.25, random_state=0, shuffle=True)
Con los datos separados y definidos, entrenamos el modelo.
lda = LinearDiscriminantAnalysis()
lda = lda.fit(train_X, train_y)
Y pasamos a la predicción y vemos el desempeño.
y_pred = lda.predict(test_X)
print("Predecidos")
print(y_pred)
print("Esperado")
print(test_y)
Predecidos
[1 0 1 0 1]
Esperado
[1 0 1 0 1]
Podemos traer una tabla de desempeño más clara y específica. Nos devuelve la precisión para predecir cada clase, promedios, predicciones correctas(recall), puntaje f1 y otros.
print(classification_report(test_y, y_pred, digits=3))
precision recall f1-score support
0 1.000 1.000 1.000 2
1 1.000 1.000 1.000 3
accuracy 1.000 5
macro avg 1.000 1.000 1.000 5
weighted avg 1.000 1.000 1.000 5
También podemos producir la matriz de confusión
ConfusionMatrixDisplay.from_predictions(test_y, y_pred)
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x2849c60e970>
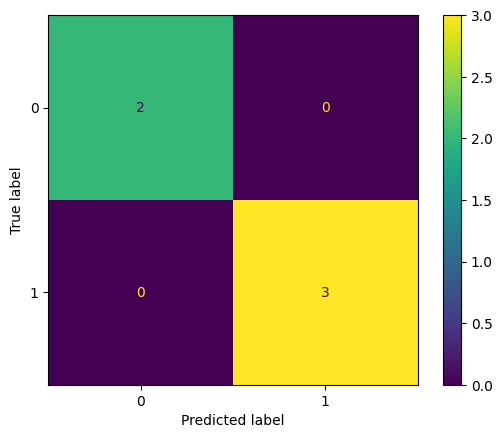
Podemos comparar con Regresión Logística, ya que solo hay 2 clases
lr = LogisticRegression(penalty = 'l2', solver='liblinear', max_iter= 1000)
lr = lr.fit(train_X, train_y)
y_pred = lr.predict(test_X)
print("Predicted vs Expected")
print(classification_report(test_y,y_pred, digits=3))
print("---------------------------------------------------------------------------------")
print(ConfusionMatrixDisplay.from_predictions(test_y, y_pred))
Predicted vs Expected
precision recall f1-score support
0 1.000 1.000 1.000 2
1 1.000 1.000 1.000 3
accuracy 1.000 5
macro avg 1.000 1.000 1.000 5
weighted avg 1.000 1.000 1.000 5
---------------------------------------------------------------------------------
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay object at 0x000002849C3C0D00>
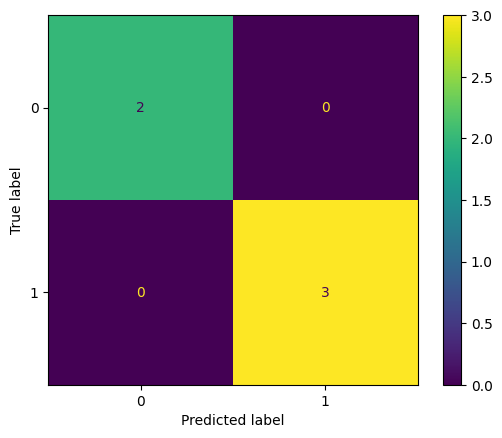
Conclusiones
- La librería SKLearn es muy buena para la fácil definición de modelos
- Nos permite fácilmente sacar reportes claros de desempeño
- En un conjunto de datos pequeños, también se pueden sacar buenos resultados, mientras las separación de las clases sea suficiente.