En el presente documento ejemplificaremos y revisaremos la aplicación de los algoritmos de regresión para la predicción de valores.
Características del modelo:
Usos: Clasificación Binaria (exclusivamente)
Representación:
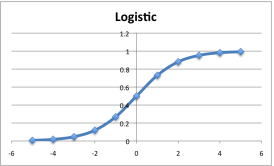
Explicación Breve: Calcula la probabilidad, o chances, por medio de la función logística
Cualidades:
- Se asume relación lineal entre atributos y objetivo
- Inestable con entrenamientos pequeños
- Inestable con clases bien separadas
Preparación de Datos:
- Reducir Ruido, Outliers y Ejemplos erróneos
- Preferir una distribución normal/gaussiana
- Se deben eliminar atributos demasiado correlacionados
Utilizaremos los siguientes datos que buscan predecir la probabilidad de un segundo ataque de corazón en pacientes según datos como edad, sexo, colesterol entre otros.
Primero importaremos las librerías necesarias y los datos:
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, classification_report, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split
input_file = "./../data/cardiac-training.csv"
df = pd.read_csv(input_file, header=0)
df.head()
| Edad | Estado_civil | Sexo | Categoria_Peso | Colesterol | Manejo_stress | Trat_ansiedad | 2do_Ataque_Corazon | |
|---|---|---|---|---|---|---|---|---|
| 0 | 60 | 2 | 0 | 1 | 150 | 1 | 50 | Si |
| 1 | 69 | 2 | 1 | 1 | 170 | 0 | 60 | Si |
| 2 | 52 | 1 | 0 | 0 | 174 | 1 | 35 | No |
| 3 | 66 | 2 | 1 | 1 | 169 | 0 | 60 | Si |
| 4 | 70 | 3 | 0 | 1 | 237 | 0 | 65 | Si |
Separamos entre entradas y salidas
X = df.loc[:, df.columns != '2do_Ataque_Corazon']
y = df['2do_Ataque_Corazon'].values
X, y
( Edad Estado_civil Sexo Categoria_Peso Colesterol Manejo_stress \
0 60 2 0 1 150 1
1 69 2 1 1 170 0
2 52 1 0 0 174 1
3 66 2 1 1 169 0
4 70 3 0 1 237 0
.. ... ... ... ... ... ...
133 54 1 0 0 170 1
134 59 1 0 0 172 0
135 55 3 0 0 122 1
136 73 2 1 1 236 0
137 62 3 0 0 185 1
Trat_ansiedad
0 50
1 60
2 35
3 60
4 65
.. ...
133 35
134 60
135 45
136 60
137 65
[138 rows x 7 columns],
array(['Si', 'Si', 'No', 'Si', 'Si', 'No', 'No', 'Si', 'No', 'No', 'No',
'Si', 'Si', 'Si', 'Si', 'Si', 'No', 'No', 'No', 'No', 'No', 'Si',
'Si', 'No', 'Si', 'Si', 'Si', 'No', 'No', 'No', 'Si', 'Si', 'No',
'No', 'Si', 'Si', 'No', 'Si', 'Si', 'Si', 'No', 'No', 'No', 'Si',
'Si', 'No', 'No', 'No', 'Si', 'No', 'Si', 'Si', 'No', 'No', 'Si',
'Si', 'Si', 'No', 'No', 'No', 'No', 'No', 'No', 'No', 'No', 'Si',
'Si', 'No', 'Si', 'Si', 'Si', 'Si', 'Si', 'Si', 'No', 'Si', 'Si',
'Si', 'Si', 'Si', 'No', 'Si', 'No', 'Si', 'Si', 'No', 'Si', 'No',
'No', 'Si', 'No', 'Si', 'No', 'No', 'No', 'Si', 'Si', 'No', 'No',
'No', 'Si', 'Si', 'No', 'No', 'Si', 'No', 'No', 'Si', 'Si', 'Si',
'Si', 'No', 'Si', 'No', 'Si', 'No', 'No', 'No', 'No', 'No', 'No',
'No', 'Si', 'Si', 'Si', 'Si', 'No', 'No', 'Si', 'Si', 'No', 'No',
'Si', 'No', 'No', 'No', 'Si', 'No'], dtype=object))
Formaremos datos de entrenamiento y datos de prueba
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.30, random_state=
0, shuffle=True)
Con esto pasamos a la construcción del modelo de Regresión Logística de sklearn y su entrenamiento
lr = LogisticRegression(penalty = 'l2', solver='liblinear', max_iter= 1000)
lr = lr.fit(train_X, train_y)
El modelo de Sklearn nos permite especificar varios aspectos del modelo que buscamos construir:
- Penalty: nos deja especificar que regularización queremos utilizar, entre L1, L2, elasticnet o ninguno.
- max_iter: la cantidad de iteraciones que permite a los resolventes a converger.
- solver: resolvente o método para hallar los coeficientes del modelo, entre LBFGS, liblinear, newton-cg, SAG, newton-cholesky o saga.
Estas configuraciones nos permiten especificar el modelo a nuestra necesidad puntual, ajustarlo a medida de pruebas y obtener el mejor resultado.
Aplicamos el modelo y evaluamos
y_pred = lr.predict(test_X)
print("Predicted vs Expected")
print(classification_report(test_y,y_pred, digits=3))
print("---------------------------------------------------------------------------------")
print(ConfusionMatrixDisplay.from_predictions(test_y, y_pred))
Predicted vs Expected
precision recall f1-score support
No 0.941 0.842 0.889 19
Si 0.880 0.957 0.917 23
accuracy 0.905 42
macro avg 0.911 0.899 0.903 42
weighted avg 0.908 0.905 0.904 42
---------------------------------------------------------------------------------
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay object at 0x0000016DFA1EAFE0>
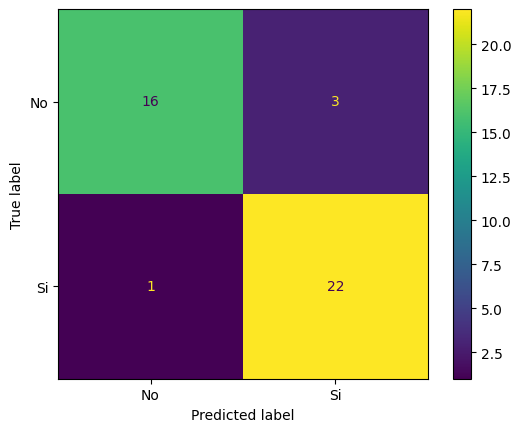
Sklearn nos permite fácilmente entrenar el modelo y aplicarlo y obtener métricas y visualizaciones del performance del modelo.
En el primer retorno podemos resaltar una precisión general del modelo de un 90,5% en general para las clases, siendo un poco mejor prediciendo gente que no sufrirá un segundo ataque (un ~94%) que las clases de que sí lo pueden llegar a sufrir (un ~88%).
Segundo podemos ver representado la matriz de confusión, que nos permite ver claramente los resultados comparados con la realidad, denotando falsos positivos, falsos negativos y aciertos. Por ejemplo vemos que se predijeron 3 falsos positivos y 1 solo falso negativo.
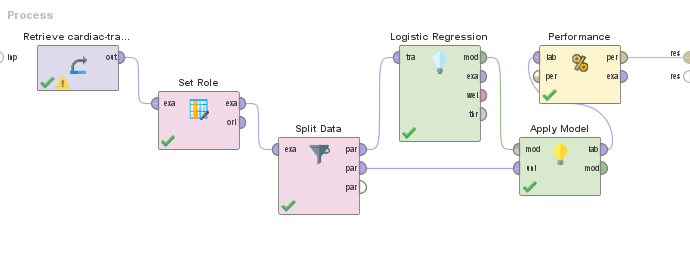
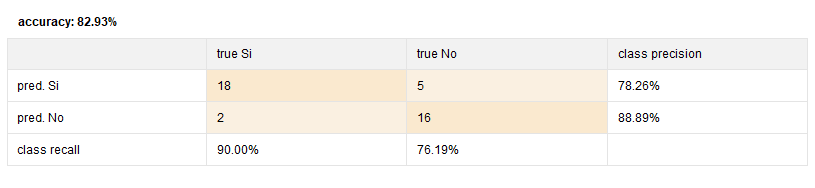
Comparación con resultados en RapidMiner
A modo de investigación, comparamos resultados del modelo entrenado en Sklearn con una aplicación equivalente en RapidMiner